- Auteur Matthew Elmers [email protected].
- Public 2023-12-16 22:27.
- Laatst gewijzigd 2025-01-24 09:32.

Wat bepaalt de nauwkeurigheid - een van de belangrijkste kenmerken van een wapen? Uiteraard van de kwaliteit van het vat en patroon. Laten we de cartridge voorlopig uitstellen, maar overweeg de fysica van het proces.
Neem een metalen staaf of buis van elastisch metaal en bevestig deze stevig in een massieve basis. Dus we krijgen een model van het apparaat dat wordt bestudeerd. Als we nu de staaf raken, maakt het niet uit op welke plaats en in welke richting, of je trekt hem terug of knijp hem in, of, ten slotte, een patroon in de buis steken en een schot afvuren, we zullen zien dat de staaf (vat) in een gedempte oscillerende beweging is gekomen. Deze trillingen worden ontleed in de eenvoudigste, en elk type van zo'n eenvoudige trilling van het vat zal op zijn eigen manier de nauwkeurigheid (nauwkeurigheid) van het fotograferen beïnvloeden.
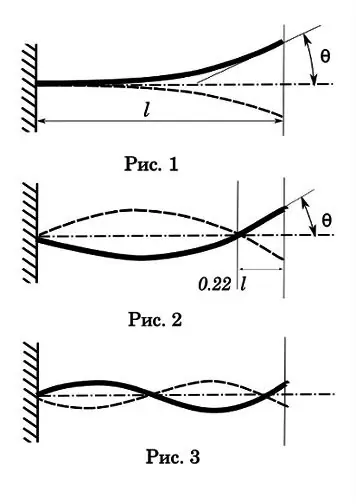
Laten we beginnen met de eerste-orde of toonhoogte trillingen. Zoals je kunt zien (Fig. 1), heeft zo'n oscillatie slechts één knoop op het bevestigingspunt, de grootste amplitude, de langste vervaltijd en de langste oscillatietijd van één periode. Deze tijd is 0,017-0,033 sec. De reistijd van de kogel door de boring is 0, 001-0, 002 sec. Dat wil zeggen, aanzienlijk minder dan de cyclus van één oscillatie, wat betekent dat dit type oscillatie geen significant effect heeft op de nauwkeurigheid van een enkel schot. Maar met automatisch fotograferen kan een interessante foto blijken. Laten we zeggen dat de vuursnelheid 1200 rds / min is, d.w.z. tijd van één cyclus - 0,05 sec. Met een eerste-orde oscillatieperiode van 0,025 sec hebben we een meervoudige frequentieverhouding. En dit is een onmisbare voorwaarde voor resonantie met alle gevolgen van dien - het wapen begint met zo'n kracht te trillen dat het uit elkaar kan vallen.
Laten we verder gaan met oscillaties van de tweede orde (Fig. 2). Maar ik stel voor dat geestesstudenten eerst een experiment doen om de tekortkomingen van het onderwijs op het gebied van natuurkunde weg te werken. Je moet een kleine jongen nemen (je kunt een meisje), zet hem op een schommel en zwaai. Voor u staat een slinger. Ga aan de zijkant van de schommel staan en probeer de jongen met de bal te raken. Na een reeks pogingen zul je tot de conclusie komen dat de beste manier om te raken is wanneer het doelwit zich in de eerste fase van oscillatie bevindt - de maximale afwijking van het evenwichtspunt. Op dit punt heeft het doel snelheid nul.
Laten we eens kijken naar het tweede orde diagram. Het tweede trillingsknooppunt bevindt zich ongeveer 0,22 vanaf het einde van de loop. Dit punt is een natuurwet, het is onmogelijk om dergelijke trillingen voor de vrijdragende balk te creëren zodat de tweede knoop op het vrije uiteinde valt. Het is waar het is en is niet afhankelijk van de lengte van het vat.
De oscillatieamplitude voor het tweede-ordeschema is lager, maar de oscillatietijd is al vergelijkbaar met de tijd van passage van de kogel door de boring - 0, 0025-0, 005 sec. Dus voor enkele opnames is dit al interessant. Om duidelijk te maken waar we het over hebben, stel je een vat voor van 1 meter lang. De kogel reist in 0,001 seconden door de hele loop. Als de oscillatieperiode 0,004 sec is, zal tegen de tijd dat de kogel de loop verlaat, de loop zijn maximale buiging in de eerste fase bereiken. De vraag voor de geesteswetenschappen is: op welk punt (in welke fase) kun je het beste een kogel uit de loop schieten om consistentie van resultaten te garanderen? Denk aan de schommel. Op het nulpunt is de vector van de stamdoorbuigingssnelheid maximaal. Het is moeilijker voor een kogel om dit punt op de loopsnede te raken, het heeft ook zijn eigen snelheidsfout. Dat wil zeggen, het beste moment voor de kogel om uit te vliegen is wanneer de loop zich op het hoogste punt van de eerste afbuigfase bevindt - zoals in de afbeelding. Dan worden onbeduidende afwijkingen in de kogelsnelheid gecompenseerd door de langere tijd die de loop in zijn meest stabiele fase doorbrengt.
Een grafische weergave van dit fenomeen is duidelijk te zien in het diagram (Fig. 4-5). Hier - t is de tijdfout waarmee de kogel de loop van de loop passeert. In afb. 4 is ideaal wanneer de gemiddelde starttijd van de kogel samenvalt met de nulfase van de looposcillatie. (Wiskundigen! Ik weet dat de snelheidsverdeling niet-lineair is.) Het gearceerde gebied is de spreidingshoek van de banen.
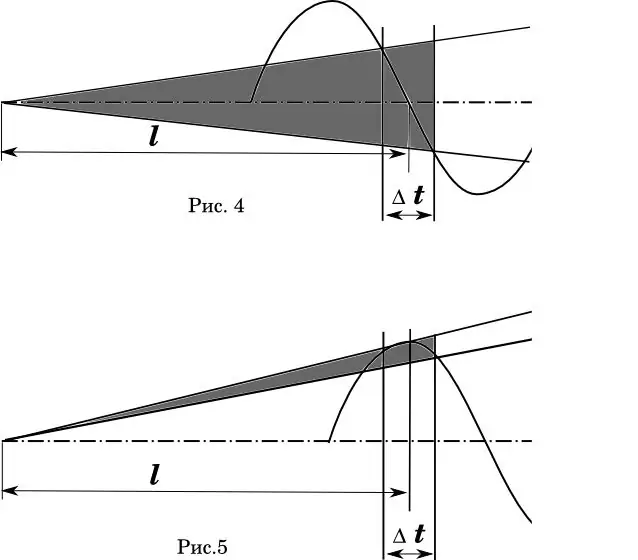
In Fig. 5 blijven de looplengte en snelheidsfout hetzelfde. Maar de fase van de loopbuiging wordt zo verschoven dat de gemiddelde vertrektijd samenvalt met de maximale doorbuiging van de loop. Zijn opmerkingen overbodig?
Nou, is het de kaars waard? Hoe ernstig kunnen de afwijkingen veroorzaakt door oscillaties van de tweede orde zijn? Serieus en heel serieus. Volgens de Sovjet-professor Dmitry Aleksandrovich Ventzel werden in een van de experimenten de volgende resultaten verkregen: de straal van de mediane afwijking nam toe met 40% met een verandering in de looplengte met slechts 100 mm. Ter vergelijking: een hoogwaardige vatverwerking kan de nauwkeurigheid met slechts 20% verbeteren!
Laten we nu eens kijken naar de formule voor de trillingsfrequentie:
waar:
k - coëfficiënt voor oscillaties van de tweede orde - 4, 7;
L is de lengte van het vat;
E is de elasticiteitsmodulus;
I is het traagheidsmoment van de sectie;
m is de massa van de romp.
… en ga verder met de analyse en conclusies.
De voor de hand liggende conclusie uit de figuren 4-5 is de snelheidsfout van de kogel. Het hangt af van de kwaliteit van het poeder en het gewicht en de dichtheid in de patroon. Als deze fout minstens een kwart van de cyclustijd is, kan al het andere worden opgegeven. Gelukkig hebben wetenschap en industrie op dit gebied een zeer grote stabiliteit bereikt. En voor de meer geavanceerde (in benchrest, bijvoorbeeld) zijn er alle voorwaarden voor zelfmontage van cartridges om de release-fase van de kogel precies aan te passen aan de looplengte.
We hebben dus een cartridge met de laagst mogelijke snelheidsvariatie. De looplengte werd berekend op basis van het maximale gewicht. De kwestie van stabiliteit rijst. We kijken naar de formule. Welke variabelen beïnvloeden de verandering in de trillingsfrequentie? Looplengte, elasticiteitsmodulus en massa. De loop wordt warm tijdens het bakken. Kan de lengte van het vat door warmte veranderen, zodat de nauwkeurigheid wordt beïnvloed. Ja en nee. Ja, aangezien dit cijfer binnen honderdsten van procenten ligt voor een temperatuur van 200 C. Nee, aangezien de verandering in de elasticiteitsmodulus van staal voor dezelfde temperatuur ongeveer 8-9% is, is het voor 600C bijna het dubbele. Dat wil zeggen, vele malen hoger! De loop wordt zachter, de buigfase van de loop verschuift naar voren op het moment dat de kogel weggaat, de nauwkeurigheid neemt af. Wel, wat zegt een doordachte analist? Hij zal zeggen dat het onmogelijk is om maximale nauwkeurigheid te krijgen op één looplengte in koude en warme modus! Het wapen kan beter presteren met een koude of warme loop. Dienovereenkomstig worden twee klassen wapens verkregen. Een daarvan is voor hinderlaagacties, wanneer het doelwit vanaf de eerste moet worden geraakt - "koud" schot, omdat de nauwkeurigheid van de tweede slechter zal zijn vanwege de onvermijdelijke verwarming van het vat. In zo'n wapen is er geen dringende behoefte aan automatisering. En de tweede klasse is automatische geweren, waarvan de lengte van de loop is aangepast aan de hete loop. In dit geval kan een mogelijke misser vanwege de lage nauwkeurigheid van een koude opname worden gecompenseerd door een snelle daaropvolgende warme en nauwkeurigere opname.
EF Dragunov kende de fysica van dit proces heel goed toen hij zijn geweer ontwierp. Ik stel voor dat u vertrouwd raakt met het verhaal van zijn zoon Alexei. Maar eerst zal iemand zijn hersens moeten breken. Zoals u weet, naderden twee monsters van Konstantinov en Dragunov de finale van de competitie voor een sluipschuttersgeweer. De ontwerpers waren vrienden en hielpen elkaar in alles. Dus het geweer van Konstantinov was "afgestemd" op de koude modus, het geweer van Dragunov op "heet". Dragunov probeert de nauwkeurigheid van het geweer van de rivaal te verbeteren en vuurt zijn geweer af met lange pauzes.

Laten we nog eens naar de formule kijken. Zoals je kunt zien, hangt de frequentie ook af van de massa van het vat. De massa van de romp is constant. Maar hard contact met de voorplaat produceert een onvoorspelbare positieve feedback naar de loop. Het systeem - barrel-forend-arm (ondersteuning) zal een ander traagheidsmoment hebben (een set van massa's ten opzichte van het bevestigingspunt), waardoor dit ook een faseverschuiving kan veroorzaken. Daarom gebruiken sporters zachte ondersteuning. Hetzelfde kenmerk wordt geassocieerd met de toepassing van het principe van "geschorste loop", wanneer de voorkant van het wapen geen hard contact heeft met de loop en er stevig aan is bevestigd (het wapen) alleen in het gebied van de ontvanger, en het tweede uiteinde raakt de loop helemaal niet of raakt via een veerbelaste verbinding (SVD).
Laatste gedachte. Het feit dat het met dezelfde looplengte onmogelijk is om dezelfde nauwkeurigheid bij verschillende temperaturen te verkrijgen, geeft een uitstekende reden om je hersens te strekken. Het is alleen nodig om de lengte en/of massa van het vat te veranderen wanneer de temperatuur van het vat verandert. Zonder de lengte of het gewicht van de loop te veranderen. Vanuit het oogpunt van de geesteswetenschappen is dit een paradox. Vanuit het oogpunt van een techneut een ideale taak. Het hele leven van een ontwerper is verbonden met de oplossing van dergelijke problemen. De Sherlocks rusten uit.






